Oracle Padding Attack

환경

CBC

이 글에서 집중할 부분은 CBC의 복호화 과정이다.

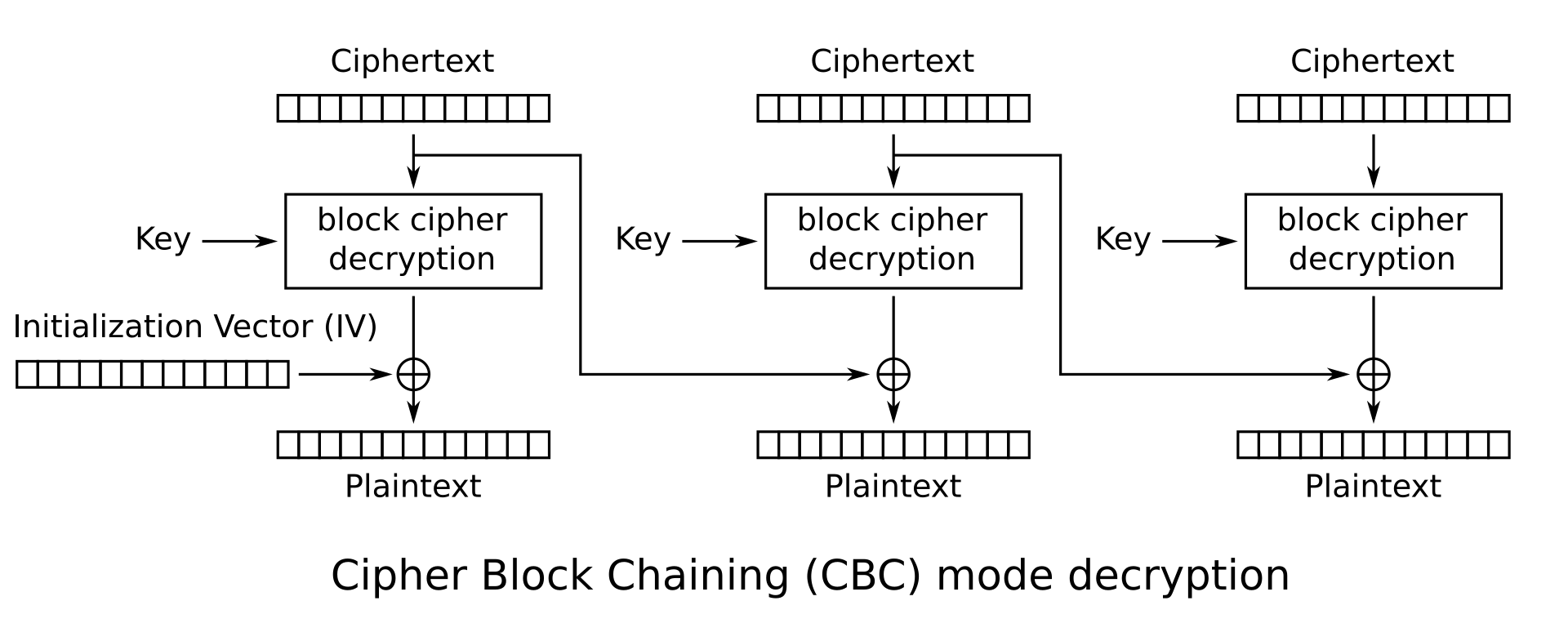
Figure 1. CBC 암호의 복호화 과정

CBC 암호는 블록 단위로 암호화를 하듯, 복호화 과정에서도 블록 단위로 다음의 XOR 연산을 수행한다:

\[P_i = D_k (C_i) \oplus C_{i-1} \\ C_0 = IV\]

즉 $i$번째 블록의 복호화은 $i$번째 블록을 풀어내는 복잡한 연산의 결과에 $C_{i-1}$을 XOR한다.

Decryption Oracle

Oracle Padding Attack은 CBC 암호의 특수한 decryption oracle이 주어졌을 때 사용할 수 있는 공격 기법이다. Decryption oracle이란 내가 암호문을 보냈을 때 평문으로 바꿔주는 역할인데, 여기서 말하는 ‘특수한’은 암호문을 넣었을 때 평문을 출력받지 못하고 계산 가능 여부만 확인할 수 있다는 조건이다. (그런 조건마저 없다면 공격할 것도 없이 암호문을 입력하면 평문이 나올 것이다) 만약 정상적인 암호문을 넣었다면 정상적으로 작동하겠지만, 형식에 맞지 않은 암호문을 넣었을 때 에러를 뱉어낸다.

패딩

블록 암호의 경우에는 블록 단위로 암호화를 시키기 때문에 블록 단위로 나누어지지 않을 경우가 발생한다. 따라서 남는 공간을 대충 채우는 과정이 필요하고, 다음의 규칙을 따른다:

n바이트의 공간이 남으면 n으로 남은 n바이트를 모두 채워버린다.

예를 들어 블록 암호가 16바이트씩 쪼개서 암호화를 시킨다고 하자. 만약에 암호화시킬 문장이 30바이트였다면, 16바이트로 한 블록을 만들고 남은 14바이트에 ‘0x02’, ‘0x02’를 붙여서 16바이트로 만들어서 블록을 저장한다.

만약에 평문이 정확히 32바이트라도 16바이트 블록 두 개를 만든 후 혼돈을 막기 위해 ‘0x10’, 즉 16짜리 바이트 16개로 모두 채운 블록을 하나 더 만들어버린다. 그러면 마지막 블록은 ‘0x10101010101010101010101010101010’가 될 것이다.

Decryption Oracle은 형식에 맞지 않은 암호문을 넣었을 때 에러를 출력한다. 즉, 입력에 대해 decryption oracle의 복호화 결과가 적합하지 않은 패딩을 가진다면 에러인데, 이 틈을 파고드는 공격 방식이 이번 글에서 소개하는 Oracle Padding Attack이다.

공격 방법

CBC 암호 방식에서 decryption oracle이 주어져 있을 때 ‘패딩’이라는 문법에 집중하는 공격

먼저 타깃이 될 암호문이 주어지고, 공격자의 목적은 이 암호문의 평문이다. 편의상 16바이트 단위의 CBC이고 암호문은 32바이트라고 해보자. 이 때 암호문의 나머지 바이트는 일정하게 유지한 채로 16번째 바이트, 즉 첫 번째 블록의 맨 마지막 바이트를 바꿔가면서 입력을 넣는다. 다 해봤자 1바이트는 256가지 경우밖에 없으므로 순식간에 처리된다.

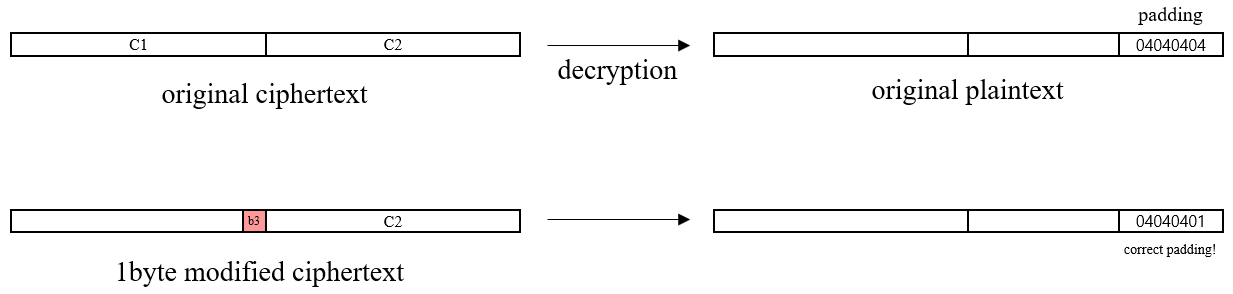
Figure 2. Oracle Padding Attack

대부분은 패딩이 틀렸기 때문에 에러를 decryption oracle에서 전달받을 것이다. 그런데 딱 하나, decryption oracle에서 에러를 뱉지 않는 경우가 존재한다. 즉, 우연히 패딩이 틀리지 않았을 경우가 발생한다. 이 때 바꿔서 입력한 바이트를 ‘0xb3’이라고 해보자.

\[P_2' = D_k ( C_2) \oplus C_1'\]

즉, 입력한 바이트를 통해 연산한 결과가 ‘0x01’, 길이 1짜리 패딩이라는 뜻이다. 따라서 $D_k(C_2)$의 마지막 두 자리를 추정할 수 있다.

\[a \oplus b = c \implies a \oplus b \oplus b = c \oplus b \implies a = c \oplus b\]

그러니까 ‘0xb3’과 ‘0x01’을 xor한 ‘0xb2’가 $D_k (C_2)$의 마지막 바이트이다.

(원래 패딩이 0x01이었으면? 바이트를 바꿔넣은 모든 경우에 대해 decryption oracle이 에러를 출력한다. 그러면 바로 평문의 맨 마지막 비트가 0x01임을 알아넨 셈이다)

이런 방법을 앞의 자리에도 적용할 수 있다. 이번에는 ‘0x02’가 두 번 나오도록 유도해야 하기 때문에 16번째 바이트를 ‘0xb2’에 ‘0x02’를 xor해서 ‘0xb0’로 고정시키고, 15번째 바이트에 대해서 모든 경우를 실험해본다. 만약 에러가 나타나지 않으면, 그 바이트를 통해 또 $D_k (C_2)$의 마지막에서 세번째, 네번째 자리를 찾아낼 수 있다.

이 방법을 16번 실행해서 $D_k(C_2)$ 전체를 알아낼 수 있다. 이말은 즉 원래의

\[P_2 = D_k (C_2) \oplus C_1\]

을 계산할 수 있게 되었다는 것을 의미하고 평문을 추정할 수 있다.

이 예시에서는 두 블록 짜리 암호문을 예로 들었는데, 블록이 많아도 문제가 전혀 되지 않는다. 뒷부분 블록은 앞의 복호화에 영향을 주지 않기 때문에 그냥 빼버리고 예시에서 했던 것처럼 마지막 블록을 반복해서 찾아내면 된다.